Avoiding Pitfalls In Periodic Orbits of Maps With A Piecewise Approach

Numerical computation is widely recognized to be of great importance in many fields of science. Many conclusions in nonlinear science and complex systems have been drawn upon simulation on a digital computer. Although this importance is widely recognized, the way of computers work is, in general, not known in detail.

Let us start our discussion with the following example. Let be the following equation, known as a logistic map:

The idea behind this equation is very simple. We start a simulation at stage k = 0. In this stage, we have our initial condition. Suppose that r = 4, and 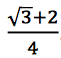It is easy to calculate that in the next stage, we will get ¼. After the third iteration, the correct answer is going to be stuck — fixed — with the value of ¾.

Using a commercial software, we proceed with this calculation, and we can get the results in Figure 1. The red line and the black line are produced by the equations F(x_k) = 4x_k(1 – x_k), while G(x_k) = 4x_k – 4x²_k. Although the equations are mathematically equivalent, the computer produces a stable and fixed result for F and a chaotic behavior for G. Nonlinear dynamic theory and a branch of math based only on calculus and differential equations cannot explain this properly.

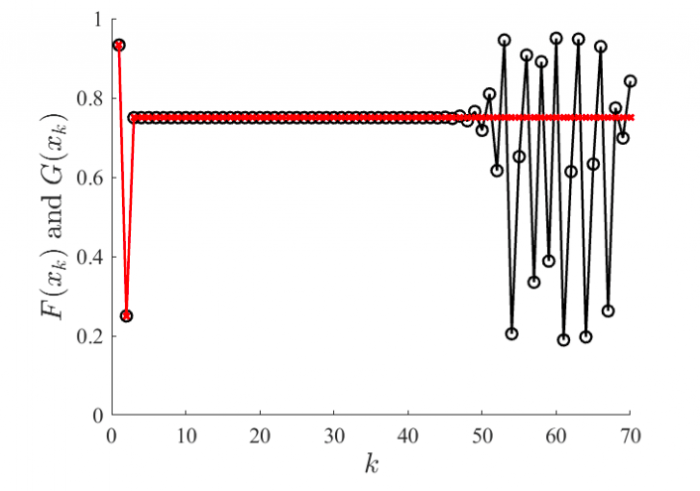
Figure 1: Simulation of the logistic map from two different computer realizations. Image courtesy Erivelton Geraldo Nepomuceno

In our recent study entitled “Interval computing periodic orbits of maps using a piecewise approach,” we recognize this situation and developed an approach to, at least, decrease this situation. The basic idea relies on the fact that the majority of numerical computations based on floating-point are built to guarantee a good result, or, in technical terms, a result within a precision according to the number of bits used, only for basic arithmetical operations.

The example in Figure 1 presents two features that turn this example in a very challenging one. First, the computation is a set of basic arithmetic operations. Second and most important, there is a recurrence where a very tiny error in the beginning grows exponentially. In our paper, we examine some features of the function, which allows us to set bounds of the result with more consistency than other approaches. The function is seen as a piecewise function. In general, the proposed method has produced intervals that are significantly narrower than those obtained by Intlab (a Matlab toolbox) approach. However, it is also clear that our method requires a significantly larger number of iterates.

Related Study

In an accompanying article published in the same journal “Detecting unreliable computer simulations of recursive functions with interval extensions,” https://doi.org/10.1016/j.amc.2018.02.020, we used such ideas to show that some previous results that guarantee long simulations on a computer are not valid for current software and hardware. We also exploit the error propagation to compute the Lyapunov exponent, a usual feature to identify chaotic systems, in the article “Computation of the largest positive Lyapunov exponent using rounding mode and recursive least square algorithm”, https://doi.org/10.1016/j.chaos.2018.04.032.

Future Directions

We are confident that computers are incredible tools to develop science and technology. But we are also confident that we must understand the way that they work in order to be able to analyze and avoid pitfalls.

These findings are described in the article entitled Interval computing periodic orbits of maps using a piecewise approach, recently published in the journal Applied Mathematics and Computation. This work was conducted by Erivelton G. Nepomuceno, Heitor M. Rodrigues Junior, and Samir A.M. Martins from the  Federal University of São João del-Rei, Matjaž Perc from the University of Maribor and Beihang University, and Mitja Slavinec from the University of Maribor.