Can one access properties of human cells in vivo? Imaging deeply inside human bodies is possible with magnetic resonance imaging (MRI), but its spatial resolution is limited to about a millimeter, i.e., 2-3 orders of magnitude coarser than the size of cells and organelles, which does not leave much hope for their direct visualization.
The challenge of accessing cellular properties is thus equivalent to building a super-resolution MRI, where understanding and modeling the cellular-level origins of the MRI signal enables mapping cellular properties indirectly, via the quantities averaged over the MRI voxels.
A paradigmatic example can be given by a method called vessel size imaging, where understanding the transverse NMR relaxation enables evaluation of the mean capillary caliber (about 10 micrometers) within each imaging voxel (of about 2 mm in each dimension). The core of this approach is the theory that relates the capillary size to the measurable signal attenuation.
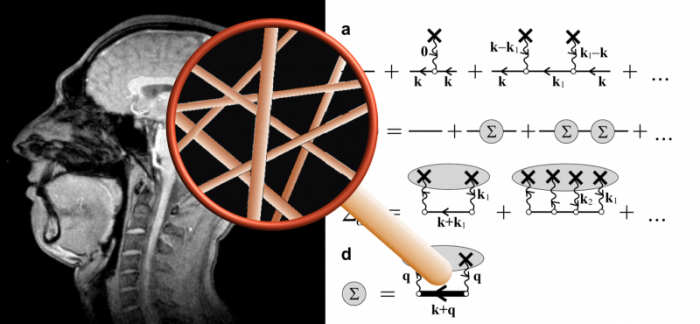
(i) My profile as seen in MRI, (ii) the magnifying glass that symbolizes the superresolution obtained via theory of the relaxation effect of capillaries (described as randomly positioned cylinders), (iii) Some theoretical equations underpinning the effective medium theory and shown as Feynman diagrams. Credit: Valerij G. Kiselev
The insights from statistical and condensed-matter physics-inspired theory of transverse relaxation at the cellular scale dictate the development of MRI measurement techniques and data interpretation frameworks. Practically, transverse NMR relaxation becomes sensitive to the tissue microstructure when some components of tissue architecture have a distinct magnetic susceptibility. These can be, e.g., deoxygenated red blood cells, cells with iron deposition, or blood doped with a paramagnetic agent for clinical examinations — enabling the sensitivity to the capillary sizes. When exposed to the strong main field of an MRI scanner, such tissue structural units induce a secondary magnetic field, which affects the phases of nuclear spins in their vicinity, and thus the overall signal.
The topical review article by Kiselev and Novikov gives an up-to-date overview of the theory of mesoscopic transverse relaxation that underlies the above methods and is considered as one of a few ways to access the tissue properties on the cellular level, the so-called tissue microstructure. The main focus of theory development is the way how the tissue microstructure affects the transverse relaxation, the process called the transverse relaxation, or dephasing.
It is a gift of nature that the typical diffusion length of spins’ host molecules during a typical MRI signal acquisition varies from a few to a few tens of micrometers, which is commensurate with the cellular or capillary dimensions. The spin motion thus samples the geometry of the cellular environment, which is imprinted in individual proton NMR signals adding up into the acquired signal. It is clear that many features of cellular organization are lost in this effective averaging over a macroscopic imaging voxel, and it is the main goal of theory to find the relevant tissue features that survive this averaging. Building an effective-medium theory of NMR relaxation is hence directly analogous to finding the relevant degrees of freedom in the renormalization group treatment of transport phenomena in condensed matter physics.
The variety of conditions possible in MRI measurements demand a variety of methods. Weak secondary fields are taken into account by the perturbation theory for the propagator of Bloch-Torrey equation describing nuclear magnetization in the presence of spatially-varying magnetic field. Moderate fields pose the challenge of going beyond the perturbative approach, which is common in physics. This can be partially fulfilled by the self-consistent Born approximation, which is equivalent to summing up an infinite subset of Feynman diagrams for the propagator. The effect of strong fields is tractable in some cases using an analog of the virial expansion in statistical physics. Beyond the relaxation theory, the authors describe in-vivo applications, discuss common misconceptions and pitfalls, and outline unresolved problems.
These findings are described in the article entitled Transverse NMR relaxation in biological tissues, recently published in the journal NeuroImage. This work was conducted by Valerij G. Kiselev from the University of Freiburg & Dmitry S. Novikov from the NYU School of Medicine.
Technical note about principles of NMR in biological samples
The MRI signal is proportional to the electromagnetic induction from nuclear magnetic moments that are subjected to the Larmor precession in the strong external field, typically created by superconductive magnets. Coherent precession gives rise to a large signal, while the loss of coherence is observable as the signal attenuation, the process called the transverse relaxation or dephasing. The spins move around, being carried by the diffusing host molecules. The dispersion in accumulated precession phases leads to dephasing. While the so induced transverse relaxation adds on the top of the contribution from the fast random molecular rotation, there is a principal difference between them. The correlation time of molecular rotation is very short (picoseconds), which renders any MRI measurement performed within tens or hundreds of milliseconds in the extremely long-time regime in which the relaxation rate is constant by the virtue of the Central Limit Theorem. In contrast, the relaxation time of molecular motion on the cellular level covers the range from the milliseconds upwards.
By varying the measurement technique and depending on the examined tissue, one can observe the transition from the short-time regime to long times, which contain more microstructure-related information than the limiting cases alone.









