A Biased Regression, A Russian Conspiracy, And Type I Errors In The World’s Oldest People

For more than two decades, scientists have argued over a pattern of human mortality. The rate at which humans physically decay with age, as measured by death rates, appears to slow or stop in old age.

However, recent findings have revealed this idea to be flawed (Newman, 2018a). The pattern results from simple errors and, in at least one case in Science (Barbi et al., 2018), the result of heavily biased statistics (Newman, 2018b).

As humans become older, their odds of dying double at a relatively fixed rate. This population-level measure of aging is called actuarial aging and reflects the physical decay of human bodies.

From puberty onwards, the odds of dying in a given year (or hour, minute, or second) double with age at a relatively fixed rate. This rate is, unimaginatively, known as the “mortality rate doubling time”: a metric that reflects the time it takes for aging to make you physically “twice as bad” at survival.

However, previous observations of a late-life “plateau” of mortality rates disrupt this pattern. As the name suggests, many researchers have observed a mortality “‘plateau” in humans after age 80, where the probability of dying no longer doubles at a fixed rate.

Instead, after age 80, the odds of dying seem to increase more slowly with age, and sometimes stop increasing altogether.

Credit: Saul Newman

This finding suggests that the aging process slows or even halts in advanced old age, and was seen as a revelation for anti-aging researchers. For scientists, and no small number of quacks, the slowing down of actuarial aging sparked many complex evolutionary, statistical, and physiological theories. The possibility that human aging stops or slows in old age even promoted fringe ideas: that human life may be extended indefinitely if we could just understand the basis of this “halt” in the aging process.

However, of course, human lifespan data must come from somewhere. For individuals older than 80, the data comes from paper records. The observed “plateaus” in human mortality data depend on a tiny percentage of these paper records: at best, a few thousand documents, drawn from the collective hand-written records on hundreds of millions of lives.

These records are, unsurprisingly, prone to errors. Mortality records depend on the handwriting of long-dead civil servants, at best, and are notoriously unreliable at advanced ages. For example, Carrie White was formerly the world’s oldest woman: her documents endured decades of scrutiny before her record was revealed to be a simple clerical error.

Documents of lifespan are a mix of century-old paper records. Out of a few hundred million cases, we should expect a few outliers. Documents can be stolen, forged, mixed up, and lost. Identities can be mistaken, or acquired by (similar-looking) younger relatives.

Worse, direct financial incentives exist for fabricating records and generating exaggerated ages. Identity theft, which remains common, can fail to be detected. Less elaborately, deaths can remain unreported.

For instance, on his 111th birthday, Tokyo’s oldest man was discovered to have been dead for over thirty years. His family had been collecting his pension by simply neglecting to report his death. The case sparked independent investigations that revealed at least another 230,000 missing or dead centenarians were “living” in Japan, including Japan’s oldest “living” person.

These findings raised a simple question: what happens to old-age patterns when errors in age reporting are introduced?

The surprising answer to this question is that late-life mortality plateaus can be generated by random errors alone, even at incredibly low rates.

Even worse for the proponents of the mortality “plateau,” observed error rates are an excellent predictor of the size of late-life plateaus. Populations with the best records have the smallest, or no, slow-down in mortality rates after age 80, and have no mortality plateau. As record quality improves, mortality plateaus diminish and then disappear.

There is no clear biological explanation for this pattern.

These findings suggest the clockwork pattern of aging is being obscured at advanced ages by simple empirical errors, which produce a fake plateau. Correct for observed error rates, and the mysterious “plateau” in old-age mortality disappears.

However, this simple explanation is unlikely to halt research on mortality plateaus in humans.

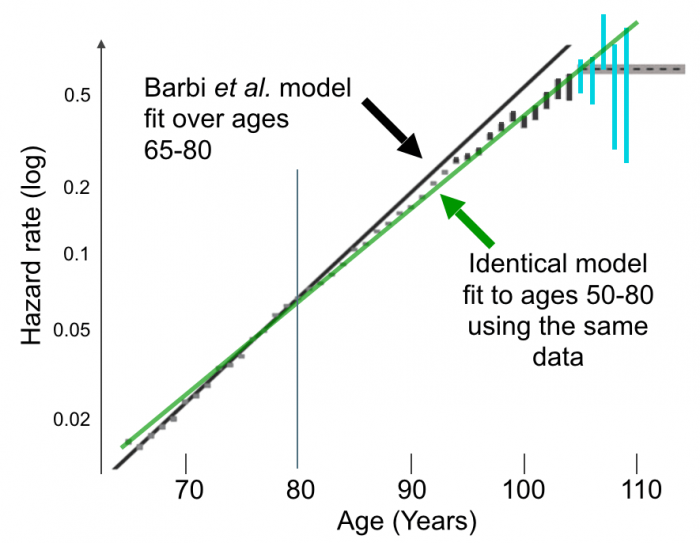
In late 2018, a Science paper was printed claiming a “clean” case of a mortality plateau, in which the data were “real” (Barbi et al., 2018). The initial results appeared robust and compelling: in their first figure, a line was fit to data in Italy showing a clear slowing-down of mortality rates after age 80 (Figure) and, after age 105, another regression was fit that appeared to show a flat late-life mortality pattern in over 3,000 individuals.

Regrettably, the authors may have had their thumb on the scale.

The model projected to fit the age 80 data was enormously biased. Of over 850 model parameters that could have been used to fit this model, the Science paper’s authors selected the single most biased set of parameters, which produced the single worst model fit. Perhaps not coincidentally, these parameters also (artificially) generated the single largest late-life plateau.

Fitting an identical model to the same dataset, using unbiased parameters, eliminates the Italian late-life plateau and improves the overall model fit (Figure). It also eliminates the need for a special late-life regression for the 3,000+ oldest Italians.

No late-life plateau exists if an unbiased model is chosen. Presumably, neither does a Science paper.

When confronted with the possibility that they had collected a large number of cases of pension fraud, or some other mundane error, an admission was also made that such a situation was impossible to rule out. As Ken Wachter put it, “Occasionally… a mistake will escape even a rigorous validation procedure” (Wachter, 2018). However, it was countered, such cases could not occur at high frequency because of the quality of documents involved.

The bias inherent in this argument is striking. Wachter states that a high error rate cannot occur because it is “wildly implausible” that their data would have so many undetected errors (Wachter, 2018). However, when asked to present evidence on the frequency of undetected errors, these authors admit that they cannot detect them.

So, according to the Science paper authors, some errors are undetectable using documentary evidence. However, there cannot be very many of these errors because of the documentary evidence.

Evidence that cannot detect such errors.

If such cases can be undetectable, how could Barbi et al., or anyone else, state they are rare?

This circular logic represents, to me, the levels of denial possible for demographers faced with a simple problem. Because type I error rates are unknown and can remain hidden in plain sight even at high error levels (as was seen in Japan), the oldest-old are unusable as a statistical sample.

However, even basic questions on the validity of “supercentenarian” data incur a high level of prejudice. In many ways, this response is understandable. Considerable resources have been expended on chasing “the oldest old.” In the case of Jeanne Calment, entire careers have been established on the validity of just one datum.

Scientifically, that is very shaky ground.

As a result, the defense of these data is desperate. Recent doubts about the validity of Jeanne Calment, nominally the world’s oldest woman, have even raised (absurd) suggestions of a Russian disinformation conspiracy.

However, the unreliable nature of old-age data has been made apparent before: not through a Russian influence campaign, but through an Irish one.

The Guinness world book, a compendium of trivia run by a beer company, has long singled out mortality records as especially dubious. The world’s longest fingernails, the longest pea-spitting distance, and the longest kiss are all certified without disclaimers. In contrast, the record for the oldest person has prompted repeat warnings on data quality.

Scientists would do well to heed that warning: “No single subject is more obscured by vanity, deceit, falsehood, and deliberate fraud than the extremes of human longevity.”

Unfortunately, perhaps bias needs to be added to that list.

References:

1. Barbi, E. et al. (2018) ‘The plateau of human mortality: Demography of longevity pioneers’, Science, 360, pp. 1459–1461.
2. Newman, S. J. (2018a) ‘Errors as a primary cause of late-life mortality deceleration and plateaus’, PLoS Biology, 16(12), p. e2006776. doi: https://journals.plos.org/plosbiology/article?id=10.1371/journal.pbio.2006776.
3. Newman, S. J. (2018b) ‘Plane inclinations: A critique of hypothesis and model choice in Barbi et al’, PLoS Biology, 16(12), p. e3000048. doi: https://journals.plos.org/plosbiology/article?id=10.1371/journal.pbio.3000048.
4. Wachter, K. W. (2018) ‘Hypothetical errors and plateaus: A response to Newman.’, PLoS Biology, 16(12), p. e3000076. doi: https://journals.plos.org/plosbiology/article?id=10.1371/journal.pbio.3000076.