
Virgo is one of the 12 zodiac constellations. Virgo’s name comes from the Latin word for virgin, and it is found near the ecliptic with Libra to the east and Leo to the west. Vertigo is the second-largest constellation in the sky, and the largest consolation out of all the zodiac constellations. The constellation of Virgo contains several bright stars including Spica, Zvijaca, Auva, Porrima, and Vindemiatrix.
General Facts About Virgo
Virgo is a large consolation, covering around 1300 square degrees of the sky. Most of the stars within Virgo are fairly dim, but Virgo can be easily located thanks to Spica, its bright star with a blue-white coloration. Findings Spica is easy if one simply locates the Big Dipper. Following the arc in the Big Dipper’s handle towards the southeast will lead you towards Arcturus, a bright star in the Bootes consolation. Following this arc further will lead you to Spica.
Virgo is viewable to those in the southern hemisphere during the autumn and winter, and it can be seen in the northern hemisphere during the spring and summer months. The right ascension of Virgo is 13 hours, and it has 0° of declination. It can be seen between latitudes of 80 N. and 80 S., and it is best seen around 9 PM during the month of May.
Exoplanets In Virgo
The constellation of Virgo contains some of the first exoplanets that were ever found. These exoplanets orbit a pulsar star referred to as PSR B1257+12. Pulsar stars are a type of neutron star, and they are created after a supernova occurs, with a massive star exploding and then collapsing in on itself. Pulsar stars rotate at extremely high speeds.
70 Virginis b is another one of the first exoplanets to be discovered. The planet was initially discovered in 1996, and at the time of its discovery, it was thought that the planet was in the star’s habitable zone, a region where liquid water could potentially be found on the surface of the planet. Yet later analysis of the planet found that 70 Virginis b has a nontraditional orbit that likely takes it much closer to its parent star than initially thought.
The star 62 Virginis is home to three different planets which were discovered in 2009. One of the planets has roughly 5 times the mass of Earth, the second planet six times the mass of Earth, and the third planet 18 times the mass of Earth. Because the two smaller planets fall within the range of mass between the mass of Earth and the mass of Neptune, they are considered super-Earths. The planet GJ 504b is one of the smallest planets ever photographed in orbit around a star like the sun, initially being photographed in 2013. The planet is still fairly large however, being four times the mass of Jupiter.
Chi Virginis is a star within the Virgo constellation that has one of the largest known exoplanets in its system. The planet has a mass about 11.1 times Jupiter’s mass.
Stars In The Constellation Of Virgo
Notable stars in the constellation of Virgo include: Spica, Zavijava, (β Virginis), Porrima (γ Virginis), Auva (δ Virginis) and Vindemiatrix (ε Virginis).
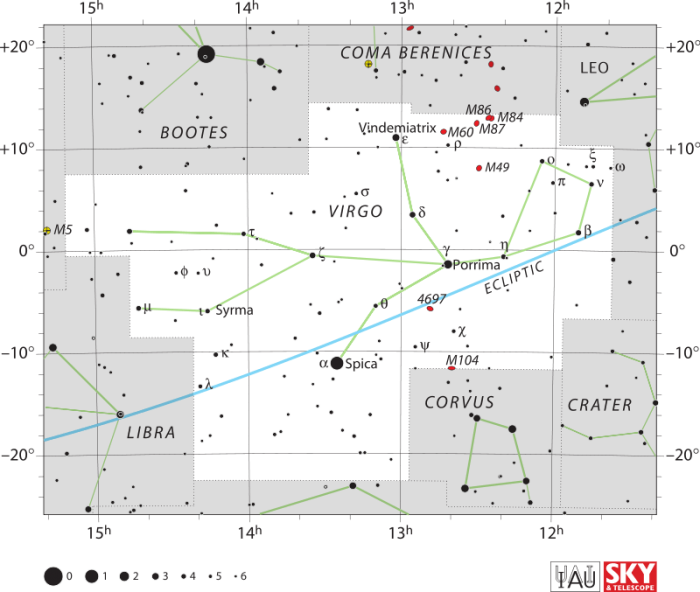
Photo: By IAU and Sky & Telescope magazine (Roger Sinnott & Rick Fienberg) – [1], CC BY 3.0, https://commons.wikimedia.org/w/index.php?curid=15412504
Spica is about 2.06° from the ecliptic, and because it is so close to the ecliptic it is sometimes occulted by planets and by the moon. Every eight years or so, Spica is passed by Venus right around the time frame of the heliacal rising. As previously mentioned, the easiest way to locate Spica is to follow the arc of the Big Dipper’s handle through Arcturus and onwards. The Spica star system has an apparent magnitude of 0.97, meaning it is quite bright and visible with the naked eye.
Beta Virginis, also referred to as Zavijava, is the constellation of Virgo’s fifth brightest star. It is found near the “head” of the constellation. Zavijava is extremely close to the ecliptic, only 0.69° North of it, so it can easily be occulted by the moon and somewhat more rarely by traveling planets. The name Zavijava comes from an Arabic word translating roughly to ‘corner of the barking (dog)’. Attempts to find substellar objects near Zavijava have found two of three potential candidates for Jovian planets. These hypothesized planets have not been confirmed at this time, though the McDonald Observatory is investigating the possibility of planets in the system, setting a limit between 0.16 and 4.2 Jupiter masses for mass. The mass of Zavijave is around 1.25 times the mass of the sun, and it has a radius of around 1.68 times the radius of the sun.
Porimma, also referred to as Gamma Virginis, is a binary star system found near the center/torso of the Virgo constellation. γ Virginis is the official Bayer designation of the star. The name Porrima refers to the Ancient Roman goddess of prophecy. In 2016, the International Astronomical Union ruled that only stars should be given proper names and not entire star systems, so the name Porrima was given to this binary star in July of 2016. The two stars in the binary star system are of roughly equivalent magnitudes, 3.65 and 3.56 respectively. The Gamma Virginis star system is about 39 light years away from the sun. The system has a mass about 1.56 times the mass of the sun.
Minelauva, also known as Delta Virginis, is a star in the constellation of Virgo that has an apparent magnitude of 3.4. At that magnitude, the star can easily be seen with the naked eye. The star gets its name from an Arabic word translating to “barking dog”. Along with Beta Virginis, Gamma Virginis, Eta Virginis, and Epsilon Virginis, the star makes up “the Barker”. Delta Virginis’ spectrum is considered an M3 III, which means that it is an evolved red giant. The outer radius of Delta Virginis is around 48 times the Sun’s radius, despite the fact that it has only about 1.4 times the Sun’s mass. In terms of luminosity, Delta Virginis has a luminosity of about 470 times that of the Sun’s luminosity. The star gives off an orange-reddish glow, and the outer envelope of the star has a temperature of approximately 4000° Kelvin. The star could be a binary star, as there is a different star, an 11 magnitude star, found at an 80-second angular separation.
Vindemiatrix, officially named Epsilon Virginis, is a star with an apparent visual magnitude of 2.8. The star is found at the end of one of Virgo’s hands. It is the third brightest star within the constellation of Virgo, and it is about 110 ly from our solar system. Vindemiatrix is a giant star that possesses about 2.6 times the Sun’s mass. The radius of the star is more than 10.5 times the radius of the sun, and approximately 77 times the Sun’s luminosity. The outer atmosphere of the star is about 5085°, and at this temperature, it gives off yellow hued light. The name of the star comes from a Latin word meaning “’the grape-harvestress”.
Beyond these vibrate stars, there are at least seven other fainter stars that have received their own names within the constellation: Heze, Zanaih, Syrma, Kang, Khambalia, and Elgafar.
The Mythological Virgo

Photo: By Sidney Hall – This image is available from the United States Library of Congress’s Prints and Photographs division under the digital ID cph.3g10067.This tag does not indicate the copyright status of the attached work. A normal copyright tag is still required. See Commons: Licensing for more information., Public Domain, https://commons.wikimedia.org/w/index.php?curid=31956870
Greek mythology has different interpretations of the constellation. Early Greek astronomers believe that the constellation was associated with Demeter, whose role as the Harvest Goddess made the constellation important during the spring. The constellation of Virgo has its roots in association with the Greek goddess of justice Dike and the daughter of the harvest goddess Demeter, Persephone. Greek mythology also holds that the world once had an eternal springtime until the God of the underworld, Hades, kidnapped Persephone. Virgo itself is tied to the concept of agriculture and fertility.
Other Constellations Near Virgo
Libra and Leo are both constellations found near Virgo. Libra is to the east of Virgo, while Leo is to the West.
Libra is one of the twelve zodiac constellations. Libra is a rather faint constellation in comparison to the other constellations of the zodiac, possessing new first magnitude stars. The brightest star within the constellation of Libra is the star called Zubeneschamali, or Beta Lobrae. Libra gets its name from the Latin term for a pair of weighing scales. Libra is best seen during the month of June at 9 PM, and it is visible between latitudes of 65° north and 90° south.
Leo is another one of the 12 zodiac constellations, representing the lion that Hercules fought in Greek mythology. It gains its name from the Latin word for lion. Leo possesses many bright stars such as a Regulus, Denebola, and Algieba. The constellation of Leo is best seen during the month of April at 9 PM, and it is visible from 90° north to 65° south. Virgo is found to the east of Leo while Cancer is found to the west.









