Rhomboidal And Triangular Four- And Five-body Problems: Planar Central Configurations

Researchers established that many stars are part of multiple–star systems. Moreover, the ratio of multiple-star systems in our galaxy is assumed to be about two-thirds. Looking at stars can lead us into believing that stars are solitary, isolated objects, but in fact, no star is born in isolation.

The stellar systems can be modeled applying the gravitational n-body problem. Central Configurations (CC’s) are a very important chapter in the gravitational n-body problems, especially of symmetrically restricted four- and five-body problems.

Particular positions of the n bodies, where the position and acceleration vectors are proportional to the same constant of proportionality define the CC’s.

They are helpful in providing explicit homographic solutions of the equations of motion and families of periodic solutions; in observing the nature of solutions near collisions and influence the topology of the integral manifolds.

The four- or five-point masses motion have been investigating when they form a rhombus or a triangle with at least one axis of symmetry. Three collinear unequal masses are on the axis of symmetry. The remaining two masses are located symmetrically on both sides of the axis of symmetry.

Three cases have been studying: firstly, four of the masses form a rhombus, and the fifth mass is placed anywhere on the axis of symmetry; secondly, the five masses will form a triangle; thirdly, as a particular case, by taking the fifth mass equal to zero, we also discuss a four-body configuration.

Regions of central configuration have been determining for various special cases of the general problem. No central configurations are possible when two pairs of masses are placed at the vertices of a rhombus and the fifth mass is placed anywhere on the axis of symmetry (except the origin).

In rhomboidal four- and five-body problems, isosceles and equilateral triangular five-body problems cases regions of central configurations are derived using analytical and numerical techniques.

Regularized equations of motion have been determining, then the chaotic behavior in the phase space by means of the Poincaré sections have been investigating. Moreover, regions with periodic and quasi-periodic orbits have been identifying.

For example, when the mass of first and third bodies are equal 1, the mass of the second and fourth bodies are equal 2, and the fifth mass is very small 0.04, we obtain the Poincaré surface of the section shown in figure 1. The inner region of figure 1 points to the existence of regular structure and some quasi-periodic orbits. Remark that in the four non-equal masses case of a rhomboidal five-body problem, when the fifth body is very small, the outer region exhibits chaotic behavior.

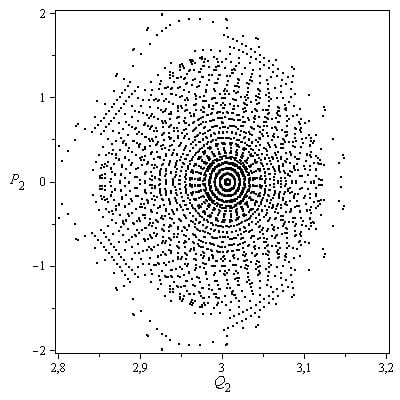
Figure 1. Examples of a Poincaré section in the rhomboidal five-body problem, when the central mass is 0.04. (Credit: Iharka Szücs-Csillik)

In the case, when two symmetrical masses m₁ = m₃=1.1 and another two symmetrical masses m₂ = m₄=1 with the central mass equal 3.15, the surfaces of section presented in figure 2 shows various types of orbits, including both circle-like quasiperiodic orbits and island orbits.

Figure 2. Example of a Poincaré section in the rhomboidal five-body problem, when the central mass is 3.15. (Credit: Iharka Szücs-Csillik)

Note the deformation in some of the circular orbits, which indicating the presence of nearby island orbits. When the central body is small, the surface of section presents very few quasi-periodic orbits surrounded by chaotic region. The increase of the central mass changes the dynamics of the problem (see figure 3).

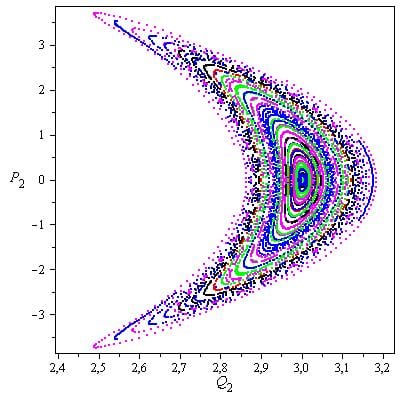
Figure 3. Example of a Poincaré section in the rhomboidal five-body problem, when the central mass is 5. (Credit: Iharka Szücs-Csillik)

The central mass increase will have a stabilizing effect on the rhomboidal five-body configuration.

These findings are described in the article entitled On the planar central configurations of rhomboidal and triangular four- and five-body problems, published in the journal Astrophysics and Space Science. This work was led by Muhammad Shoaib (Higher Colleges of Technology), Abdul Rehman Kashif (Capital University of Sciences and Technology), & Iharka Szücs-Csillik (Astronomical Institute of the Romanian Academy).