Optimal Energy Growth In Plasma Instabilities

The Sun, our closest star, is a ball of plasma interacting with a magnetic field. This interaction leads to a host of fascinating and complex dynamics. The visible yellow disk of the Sun (which should not be viewed directly with the naked eye) marks, approximately, the base of the solar atmosphere.

In the Sun’s atmosphere, magnetic field (that can emerge through the photosphere) gets buffeted, twisted and sheared until it becomes unstable and eruptions occur. These eruptions, apart from being interesting in their own right, form the basis of space weather that can interfere with the Earth’s artificial satellites and power grids. Understanding the basics of plasma instabilities and eruptions is, therefore, of theoretical and practical importance.

This article summarizes some recent new insights into a classical instability of plasma physics – the tearing instability. For the tearing instability to occur, a region called a current sheet is required, where the magnetic field changes direction over a very small length scale (see Fig 1a). Once the instability develops, the magnetic field lines ‘tear’, reconnect and from magnetic islands (Fig 1b). This instability is a key candidate for the ignition of solar flares.

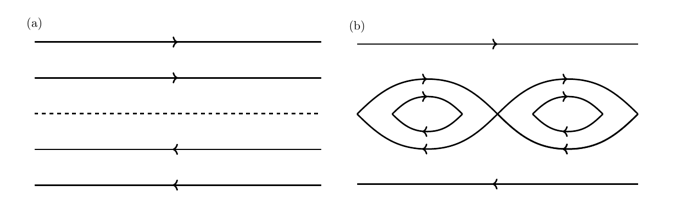
A cartoon of how the magnetic field changes due to the tearing instability. (a) shows the initial magnetic field where field lines change their direction rapidly at the current sheet (dashed line). (b) shows the magnetic islands that form, resulting in a change of connectivity of the field lines.

Since the seminal work of Furth et al. (1963), the growth rate of the onset of the tearing instability has been considered to be too slow for many solar applications. In recent years, new discoveries by physicists have revealed a fast phase of the tearing instability once the width of the current sheet reaches a critical thickness (e.g., Lourerio et al. 2007, Lapenta 2008, Pucci & Velli 2014).

From a mathematician’s perspective, the theoretical analysis of the tearing instability has, until now, focused only on a particular phase of the instability. Without going into details, the equations describing the onset of instabilities can be described as either ‘normal’ or ‘non-normal’. For a normal system, one finds the eigenvalues (characteristic numbers associated with that system), with the largest (depending on how this is measured) corresponding to the growth rate of the instability. This is the classical way of studying the onset of instabilities. For a non-normal system, eigenvalues do not give a complete description of the instability’s onset. Instead, they describe the behavior at large time scales and do not account for the possibility of significant transient growth at earlier times.

The basic (although still complicated) equations used to describe the tearing instability represent a union of fluid dynamics (the plasma is treated as an electrically conducting fluid) and electromagnetism, known as magnetohydrodynamics (MHD). The MHD equations describing the onset of the tearing instability are highly non-normal. Hence the solutions to these equations have the possibility of exhibiting large transient energy growth. If such transient growth exists, it could lead to faster dynamics than that predicted by considering only the eigenvalues of the system.

It is not the case that a non-normal system will necessarily produce large transient energy growth. Another important factor is the form of the initial perturbation that is imposed on the current sheet. To show the maximum effect, one can calculate the optimal energy growth, optimized for all types of initial perturbation. Fig 2 gives an example of the optimal energy growth for the onset of the tearing instability, for a particular set of parameters.

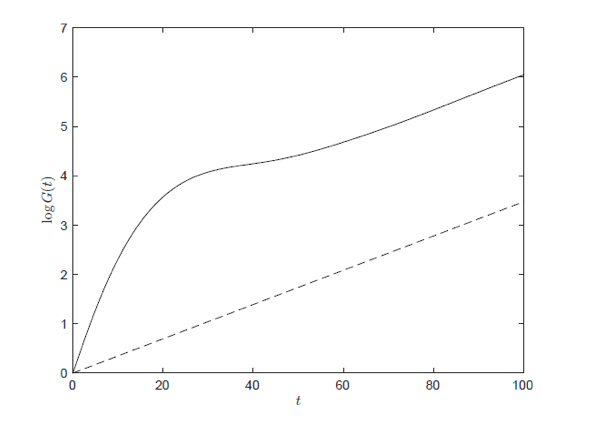
The optimal energy G as a function of time t. The dashed line is calculated using the classical analysis. The solid line takes into account the non-normal aspects of the system, missed by the classical analysis, resulting in large transient growth. Permission: Springer Nature.

The dashed line represents the optimal energy growth when only the largest eigenvalue is taken into account (the classical analysis). The solid line shows the optimal energy growth when moving beyond the classical theory and including the non-normal effects of the system. At early times, the transient growth rises very quickly producing much more energy growth (within a given time) than that predicted by the classical theory. At later times, the solid and dashed lines become parallel as the transient behavior has now decayed away and the solution is dominated by the largest eigenvalue.

This type of analysis has only recently been applied to the solar atmosphere and has the potential to greatly enhance our understanding of instabilities and eruptions on the Sun by discovering faster energy growth that previous analysis could not detect.

References:

• Finite-Resistivity Instabilities of a Sheet Pinch (1963) Furth, H.P., Kileen, J., Rosenbluth, M.N., Phys. Fluids, 6, 459.
• Self-Feeding Turbulent Magnetic Reconnection on Macroscopic Scales (2008), Lapenta, G., Phys. Rev. Lett., 100, 235001.
• Instability of current sheets and formation of plasmoid chains (2007), Lourerio, N.F., Schekochihin, A.A., Cowley, S.C., Phys. Plasmas, 14, 100703.
• Reconnection of Quasi-singular Current Sheets: The “Ideal” Tearing Mode (2014) Pucci, F., Velli, M., Astrophys. J. Lett., 780, L19.
• For more information on the mathematics of non-normal systems, the reader is directed to the monograph:
• Spectra and Pseudospectra (2005), Trefethen, L.N. & Embree, M., Princeton University Press

These findings are described in the article entitled Optimal Energy Growth in Current Sheets, published in the journal Solar Physics. This work was led by David MacTaggart from the University of Glasgow.