Finding Solutions To Contradictions In Relativity And Quantum Mechanics

The twentieth century gave birth to two of the most important Physics theories of nowadays: Special/General Relativity and Quantum Mechanics. These two theories have accompanied humanity in the questions of what is space, what is time and what is matter; they have taught us to characterize these entities.

In spite of their great successes, not everything has been smooth and kind. Relativity and Quantum Mechanics cannot be applied at the same time to the same problem. In trying to do so one arrives at contradictions. Contradictions arise from the very foundational and most primary aspects of each theory: locality, causality, and determinism in Relativity; and entanglement, anti-causal events, and probabilistic results in Quantum Mechanics. Decades of work on these aspects were first inspired by a discussion between Einstein, Podolsky, and Rosen [1], which came to be known as the EPR paradox, to do with whether or not Quantum Mechanics was a complete theory.

The contradiction is best explained in Bohm’s thought experiment [2], in which it is concluded that the results of measurements carried out on distant matter are affected by each other instantly if this matter is entangled.

Entanglement emerges in quantum mechanics when a set of two or more particles can only be described as a whole, and not as individual entities. This seems to force the state of each particle to depend on the state of the others, even when they are widely separated.

The consequences of entanglement appear to be in contrast with local causality, which is imposed on spacetime by Special Relativity: a sequence of cause and effect that constitutes a fundamental principle by which we think about and do our scientific work. What Special Relativity forces is a causal structure of spacetime in the form of light cones (cf. Fig. 1), that prevents an event to influence another event which lies outside its future light cone (cf. Fig. 2).

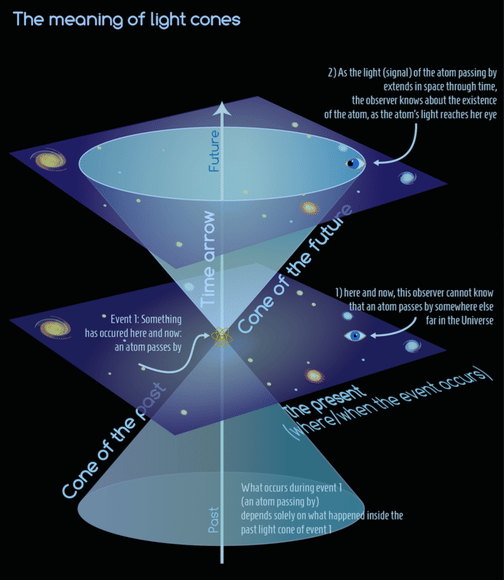
Figure 1: For one to have information about an event, a signal must be transmitted from this event onto oneself, and the fastest possible signal is light. As light travels with finite speed, it requires some time for it to travel from its source to another point; the light cone of an event refers to the space that a light signal, coming from such an event, is able to cover as time passes. An event occurring at some place and time cannot interact in any way with anything occurring outside its light cone limits, while everything that influences an event must lie inside its past light cone.

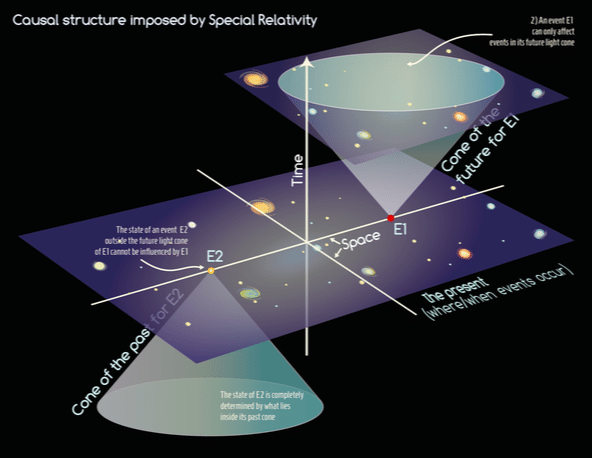
Figure 2: An event is a point on spacetime specified by one time coordinate and three spatial coordinates. In this figure, only two spatial dimensions and the temporal one are drawn. Light cones are determined by the trajectory a ray of light follows through any point in spacetime, and serve as a boundary to the set of events each point can access. Illustrated here is the causal structure of spacetime, with two events, E1 and E2, which are causally disconnected.

A proposed solution to the non-local behaviour embedded in quantum systems is the existence of hidden variables. Hidden variables are parameters which determine the behaviour of our object of study, but that we have not taken into account, and in this sense are “hidden” from us. Soon after Bohm’s thought experiment came to light, in 1964, John Bell [3] demonstrated that the hope of completing Quantum Mechanics with hidden variables was lost.

Bell constructed an inequality which every theory of (local) hidden variables must satisfy, and demonstrated that Quantum Mechanics violated this inequality, thus concluding the impossibility to explain non-local phenomena of Quantum Mechanics through local hidden variables. The consequence of Bell’s conclusion is, strange as it may seem, the fact that matter in some planet of the universe might know how to “behave”, through instructions given by matter in some other distant planet of the universe; and, furthermore, instantly!

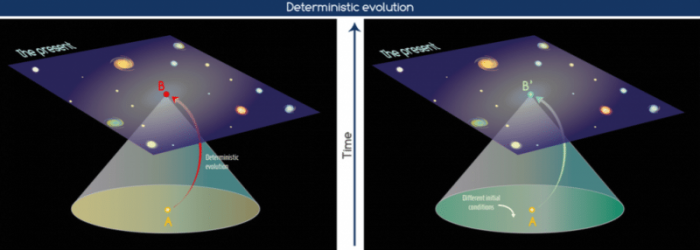
Figure 3: Deterministic evolution of the state of a system A: if different states, B and B′, result from the evolution of the same state A, different initial conditions must have taken place.

But there is still something in Quantum Mechanics that one has not accounted for: factuality, which is a consequence of determinism. In a paper recently published [4] this was taken into account. What this entails to is that a particle evolves from state A, at time t₀, to state B, at time t₁, in a deterministic way, that is, that one can predict state B given enough initial conditions, and that if state B takes place at time t₁, it is the only state that the system could have taken, given the initial conditions (cf. Fig. 3). But some of the conditions may still be hidden in the form of hidden variables, only that now evolution is truly deterministic.

So why is it that, when performing the same experiment repeatably, Quantum Mechanics does not always give the same results? In other words, why does it only provide a statistical interpretation of natural phenomena? Here we need to stress yet again the fact that spacetime is endowed with a locally causal structure. This means that everything that can affect a given event E must lie within its past light cone. At any given time t₀, then, we may only have access to initial conditions on the hypersurface t = t₀ that are enclosed within the past light cone of E (cf. Fig. 4). Any information outside this region, unknown to us, may and surely will affect the future evolution of the event.

What lies at the bottom of the authors’ formulation is that Bell made a few assump- tions to build his inequality that are not true in a deterministic scenario; when adding true determinism to the evolution of particles Bell’s inequality cannot be constructed. Now, given that Bell’s inequality cannot be constructed, the previous restriction which Quantum Mechanics must meet in order to be explained locally no longer exists.

Furthermore, one can construct a certain inequality which every deterministic local system must satisfy. This is done in the reference cited above, and it is demonstrated that Quantum Mechanics always satisfies this inequality. In this way, the authors conclude, phenomena which arise from the formalism of Quantum Mechanics can be interpreted in a local way, when adding determinism, adhering to the requirements of at least Special Relativity (if not yet General Relativity).

And what about entanglement? It is important to stress that entanglement, in a deterministic scenario, always calls for a common cause, from which the behaviour of the entangled systems arises at a given time regardless of how far away the two entangled systems are from each other. This is always possible due to the fact that the event light cones, those bridges that connect everything to their causal past, always intersect when followed backwards in time (cf. Fig. 5).

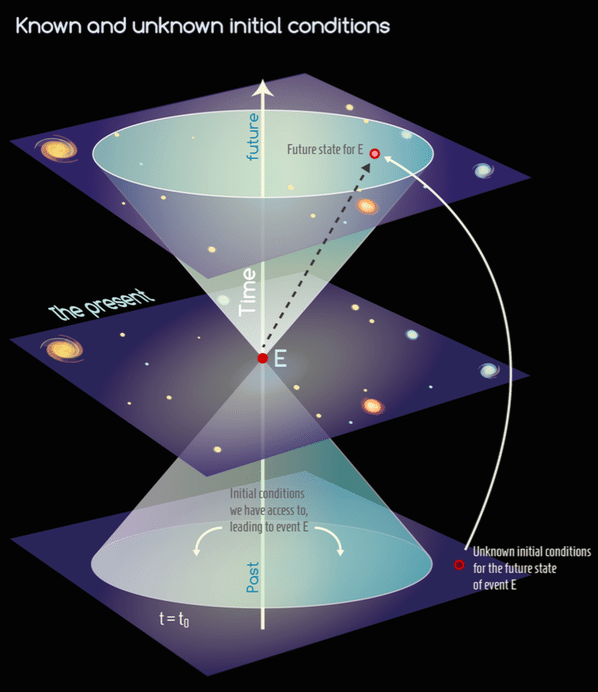
Figure 4: Initial conditions we have access to when studying an event E. The future state of E, influenced by conditions which are unknown to us.

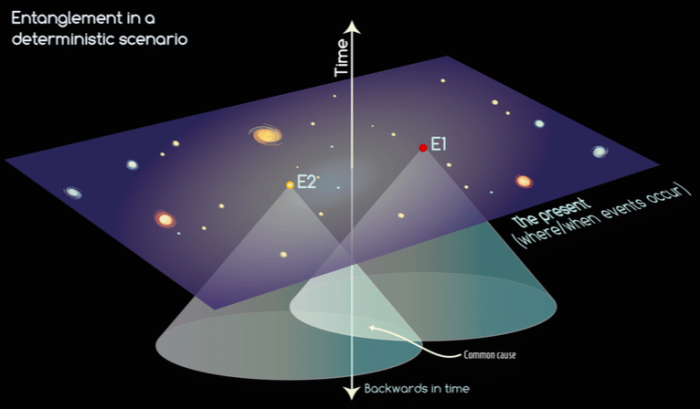
Figure 5: Two events whose light cones intersect, by going backwards enough in time.

The authors would like to thank Aline Guevara from the Science Communication Unit at ICN, UNAM, for the images in this work. This work was contributed by Natalia Sánchez-Kuntz and Eduardo Nahmad-Achar from Universidad Nacional Autonoma de Mexico.

References

1. A. Einstein, B. Podolsky and N. Rosen: Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 47, 777 (1935).
2. D. Bohm and Y. Aharonov: Discussion of experimental proof for the paradox of Einstein, Rosen, and Podolsky, Phys. Rev. 108, 1070 (1957).
3. J.S. Bell: On the Einstein Podolsky Rosen paradox, Physics 1, 195 (1964).
4. N. Sánchez-Kuntz and E. Nahmad-Achar: Quantum Locality, Ring’s a Bell?: Bell’s inequality meets local reality and true determinism, Found. Phys. 48, 27 (2018). doi: 10.1007/s10701-017-0126-z