
In the early stages of thermodynamics, researchers focused on the study of heat and work transfer. Thermal radiation, which is to be considered in various disciplines such as engineering, atmospheric science, and astrophysics, has been treated for a long time using concepts from heat theory.
Only in the last decades have scientists gradually understood that the radiation reservoirs are not characterized by their temperature only (as the heat reservoirs are) but also by other parameters such as chemical potential and view factor (see [1A]). The most successful model of thermal radiation originates from the seminal works of Planck [2A] and is based on the hypothesis of blackbody radiation (BBR).
In the last decades, many authors studied the conversion of thermal radiation energy into work, mainly due to implications for solar energy utilization. The most significant research effort has been made for the particular case of BBR, where remarkable results have been obtained. A first choice for the maximum conversion efficiency is the Carnot relationship [7B]:
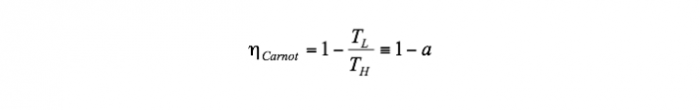
(1a,b)
where TH and TL are the temperatures of the radiation reservoir and environment, respectively. The definition of the reduced environment temperature a(≡TL/TH) has been used in Eq. (1b). Another choice is the following relation derived independently by Petela [8B], Landsberg [9B] and Press [10B] (PLP efficiency):
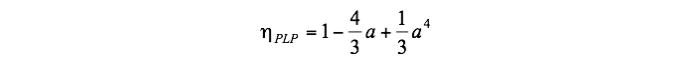
(2)
It has been proven recently that these upper bound efficiencies, which are functions only of the temperatures of the radiation reservoir and environment, are not general. Indeed, radiation reservoirs are characterized by other parameters in addition to temperature and any difference in the values of these parameters is expected to yield a difference in the conversion efficiency value. For instance, the Carnot and PLP efficiency are appropriate only for hemispherical reservoirs of BBR [11B,12B,18A]. More general upper bound efficiency formulae have been derived in [11B,12B] for BBR reservoirs of arbitrary view factor and Carnot and PLP efficiency are just particular cases [18A]. For instance, in case the BBR reservoir is seen from the radiation energy converter under a geometric (view) factor fH, an upper bound for the conversion efficiency is [11B,12B]:
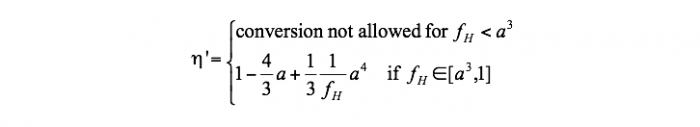
(3)
The constraint fH > a3 comes from the assumption of a hypothetic energy conversion process with no entropy generation. In the particular case fH = a3, Eq. (3) reduces to the Carnot efficiency Eq. (1a,b). For hemispherical BBR reservoirs fH = 1 and Eq. (3) reduces to the PLP efficiency Eq. (2). The upper bounds η’ works for radiation energy conversion into work, the same role that the Carnot efficiency plays when heat conversion into work is considered. Indeed, despite the fact that the Carnot efficiency depends just on the hot and cold heat reservoir temperatures, it is higher than the efficiency of a real heat engine in an arbitrary operation regime.
Blackbody radiation is a useful theoretical tool. However, in nature, the mean occupation number per photon energy level rarely corresponds precisely to that of blackbody radiation. In these cases, thermal radiation is better modeled as diluted BBR. Well-known examples of diluted thermal radiation are diffuse solar radiation and the radiation emitted by a gray solar thermal collector. Diluted BBR is characterized by the dilution factor ε < 1. Solar radiation outside the Earth’s atmosphere may be modeled as undiluted blackbody radiation (ε = 1). Solar radiation on the Earth’s surface is either direct radiation (coming directly from the direction of the Sun) or diffuse radiation (received from different regions of the celestial vault, after several scatterings). Due to absorption, both direct and diffuse solar radiation may be modeled as diluted BBR, with dilution factors which are generally different from each other.
The thermodynamics of diluted BBR has been treated in seminal papers by Landsberg and Tonge [14B,15B]. In the last decades, several authors used these works in studies on the physics of multiply scattered solar radiation in the atmosphere [16B], analysis of entropy fluxes transferred by conduction and radiation [17B], atmospheric processes [18B,19B], interaction of thermal radiation with a surface [20B], and estimation of the exergy of solar radiation at ground level [21B].
However, conversion of diluted BBR energy into work has been rarely considered. Note that the Carnot and PLP efficiencies may optimistically predict positive values in cases when the radiation energy converter receiving diluted BBR energy cannot generate work.
In a recent paper, we developed a simple model for the work extraction from a high-temperature reservoir of diluted BBR, the sink being a heat reservoir. Most relevant processes are included into the model, and the irreversibilities of these processes are taken into account. Upper bounds for the efficiency may be obtained under the hypothesis of fully reversible energy conversion.
By relaxing the reversibility assumption, more accurate (i.e. lower) upper bounds are obtained [21A]. This is a direct consequence of the Gouy-Stodola theorem [1A]. The particular case of gray body radiation has been considered. A few details follow. The absorber receives diluted radiation of dilution factor εH from a radiation reservoir. The absorptance of the absorber is αa and the absorber emits a diluted BBR of dilution factor εa under the geometric factor fa. The key parameter is the interaction factor ι defined by:
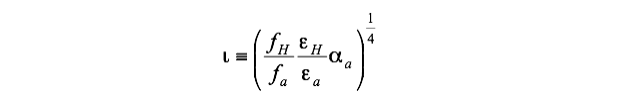
(4)
The important result is the following upper bound efficiency η++:
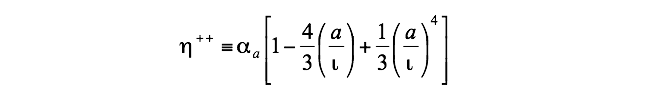
(5)
η++ constitutes an analytical upper bound efficiency for the conversion efficiency of a radiation energy converter operating between a high-temperature radiation reservoir of diluted radiation and a low-temperature heat reservoir. η++ may be used for a large class of situations characterized by α ≤ ι ≤ 1; this class includes the situation for which the PLP efficiency has been derived (namely the very particular case when the energy of undiluted and fully concentrated BBR is absorbed by using blackbody absorbers emitting hemispherically, for which ι = 1). η++ is more accurate than the Carnot and PLP efficiencies. The upper bound efficiency η++ depends on the hot and cold heat reservoir temperatures as well as on the dilution factor and the geometric factor of the radiation reservoir and on the nature of the absorber (i.e. absorptance, emittance, geometric factor of emitted radiation). But η++ is higher than the efficiency of any real radiation energy converter into work.
These findings are described in the article entitled How much work can be extracted from diluted solar radiation? recently published in the journal Solar Energy. This work was conducted by Viorel Badescu from the Polytechnic University of Bucharest and the Romanian Academy.
References:
- [1A] V. Badescu, Lost available work and entropy generation: Heat versus radiation reservoirs, J. Non-Equilib. Thermodyn. 38 (2013), 313–333.
- [2A] M. Planck, The Theory of Heat Radiation, Barth, Leipzig, Germany, 1913 (English translation by M. Masius, P. Blakiston’s Son, Philadelphia, Pa., 1914; English translation by M. Masius, Dover, New York, 1959.)
- [18A]V. Badescu, Maximum reversible work extraction from a blackbody radiation reservoir. A way to closing the old controversy, Europhys. Lett. 109 (2015), 40008.
- [21A] V. Badescu, Accurate upper bounds for the conversion efficiency of black-body radiation energy into work, Phys. Lett. A, 244 (1998), 31-34.
- [7B] S.M. Jeter, Maximum conversion efficiency for the utilization of direct solar radiation, Sol. Energy 26 (1981), 231–236.
- [8B] R. Petela, Exergy of heat radiation, Journal of Heat Transfer 86 (1964) 187–192.
- [9B] P.T. Landsberg, J.R. Mallinson, Thermodynamic constraints, effective temperatures and solar cells. Coll. Int. sur l’Electricite Solaire. Toulouse: CNES, 1976, pp. 27–35.
- [10B] W.H. Press, Theoretical maximum for energy from direct and diffuse sunlight, Nature 264 (1976) 734–735.
- [11B] V. Badescu, Is Carnot efficiency the upper bound for work extraction from thermal reservoirs? Europhys. Lett., 106 (2014), 18006.
- [12B] V. Badescu, How much work can be extracted from a radiation reservoir? Physica A, 410 (2014) 110-119.
- [14B] P.T. Landsberg, G. Tonge, Thermodynamics of the conversion of diluted radiation, J. Phys. A Math Nucl. Gen., 12 (1979), 551 – 562.
- [15B] P.T. Landsberg, G. Tonge, Thermodynamic energy conversion efficiencies, J. Appl. Phys., 51 (1980), R1 – R20.
- [16B] V. Badescu, Maximum conversion efficiency for the utilization of multiply scattered solar radiation, J. Phys. D: Appl. Phys., 24 (1991), 1882-1885.
- [17B] S.E. Wright, Comparative analysis of the entropy of radiative heat transfer and heat conduction, Int. J. Thermodyn., 10 (2007),27 – 35.
- [18B] W. Wu, Y. Liu, A new one-dimensional radiative equilibrium model for investigating atmospheric radiation entropy flux, Phil. Trans. R. Soc. B 365 (2010), 1367–1376.
- [19B] W. Wu, Y. Liu, Radiation entropy flux and entropy production of the earth system, Reviews of Geophysics, 48 (2010) RG2003.
- [20B] S. Kabelac , R. Conrad, Entropy Generation During the Interaction of Thermal Radiation with a Surface, Entropy, 14 (2012), 717-735.
- [21B] M. Neri, D. Luscietti, M. Pilotelli, Computing the Exergy of Solar. Radiation From Real Radiation Data, ASME J. Energy Resour. Technol., 139, 061201 (2017)









