Celestial Mechanics, Relative Equilibria, And Many Difficult Problems

Celestial mechanics is a branch in the intersection of mathematics and physics, where the main goal is to describe the motion of any number of bodies (in a three dimensional space), characterized by some physical attributes like mass or electric charge and with some specific geometrical form, which interact each other by a law dependent of the previous factors. All this is usually called a system of particles.

To start work with a system of particles, once the geometry and properties of the bodies involved have been established, the next step is precise a mathematical function that represents the law of interaction of the bodies, which is called the potential function. At this point, a system of equations is obtained which involves positions, velocities, and accelerations. With all above, the one interested in attacking such a problem might just have to start praying…

The more usual situation study in celestial mechanics is known as the N-body problem, where are N point masses, i.e., bodies perfectly spherical and with mass as a single physical property, denoted by m₁, …, m_N moving in a d-dimensional Euclidean space, although we will be most interested in the cases d = 2 and 3. If the locations of the masses are written as x₁, x₂, …, x_N,
and we let r_ij = ∥x_i − x_j ∥ denote the distances between mass i and j. The interaction between the bodies is given by the Newtonian potential:

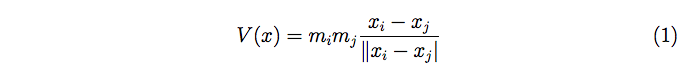
Then the equations are:

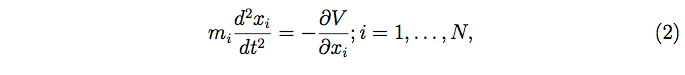
Equation (2) is usually called the N-body equations, Newton’s equations, or the N-body problem (Meyer et al., 2009). The history of the N-body problem has nearly three centuries of contributions from some of the most brilliant minds, from Newton to Poincare. But this is not the most fascinating feature of this problem.

After all, equation (2) has been solved only for N = 1 and N = 2, but the N-body problem is an open problem when considering three or more bodies. Anyone seduced by celestial mechanics could start to imagine configurations of three objects moving in space: for example three stars, or a star, a planet and a satellite, or the nucleus of a Helium atom together with its two electrons. As we said before, the spatial positions of these points are represented by three vectors x₁, x₂, x₃, and the masses of the objects are denoted m₁, m₂, m₃. The masses move so that their positions x_i are functions of time t.

Under these conditions, equation (2) is rewritten as:

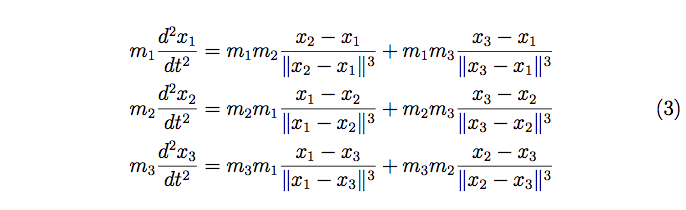The right-hand sides should be multiplied through by a very famous physical constant, the Newton’s Universal Constant of Gravitation, denoted G. But in mathematics, through a rescaling, we allowed to set G = 1. For N = 1 and N = 2 with some simple tools of calculus proved that the trajectories of the bodies must be some kind of conic, but then, for N = 3, what are all the possible trajectories?

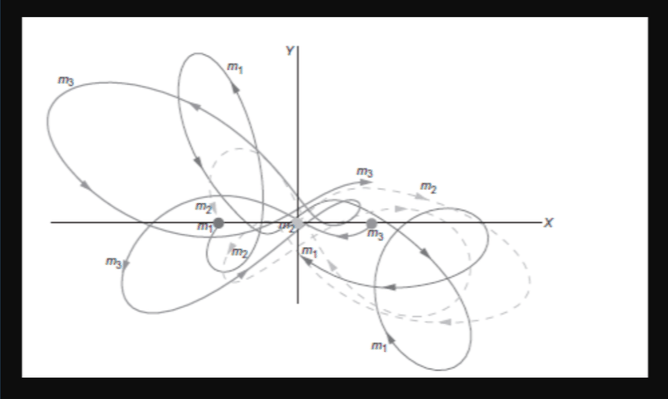
Figure 2: The three body problem is considered the first example of a chaotic system, as very few analytical solutions are known for this problem. Credit: John A. Arredondo

The previous question is so hard, that it has only been possible to get an answer for some particular situations: equals masses, specific configurations of the bodies, and so on. One of these special configurations was established by Euler and Lagrange and is called the “Problem of the Relative Equilibria,” a configuration of the bodies where they remain in equilibria in a rotating system or a configuration where position and acceleration vectors are proportional, with the same constant of proportionality.

This particular problem is similar in awkwardness to the general N-body problem, as it is still open for N ≥ 6. But the multiple applications of such configurations, especially in the design of trajectories for spatial journeys, motived Steve Smale to include in their list of problems to be solved in the 21st century (Smale, 2000). In this list, as the sixth problem stated, we must prove the finiteness of the number of relative equilibria in celestial mechanics.

To find relative equilibria or, more generally, some result for the N-body problem, is not only of mathematical interest but is also very important in applications. Thus, the description of the system of particles must be as accurate as possible, but the potential function in equation (1) works only for spherical bodies. Moreover, we know that the equations of classical mechanics fail to describe the behavior of, for example, the perihelion advance of Mercury. So, what can we do? Two questions appear:

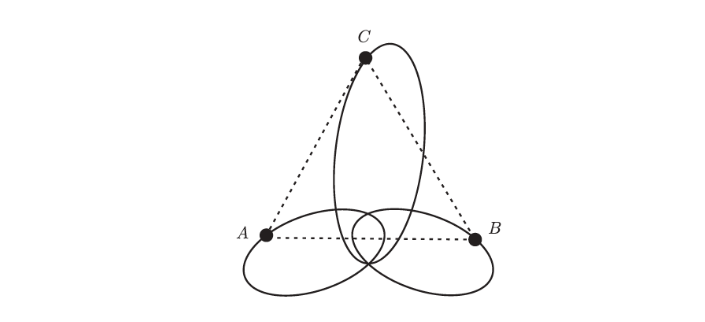
Figure 3: Lagrange found a solution for the three-body problem where each body moves in an elliptical trajectory while the three bodies preserve an equilateral triangle configuration. Credit: John A. Arredondo

1. How to model (for example) a satellite orbiting the Earth, knowing that Earth, and planets in general, are far from being perfectly spherical objects.

2. The physical theory that generalizes Newtonian mechanics is general relativity. Then, why not use this to achieve a better description of the dynamics of the planetary system and objects like quasars, galaxies, and black holes?

The answer to the first question, we need to find a potential function for every specific problem. This is done by solving the Poisson equation, which is a difficult problem in partial differential equations, from which is known that the simplest potential function is that for interaction between spherical bodies (Arredondo et al., 2012).

For the second question, unlike Newtonian mechanics, in general relativity, even the simplest case of a two-body problem cannot be solved.

A way to overcome the obstacles described above is to seek a continuous, classic description of the problem, but with an effective potential: a potential function which is consistent with the experimental observations. Doing this, we get an N-body problem where the interaction between the bodies is described by a potential of the form:

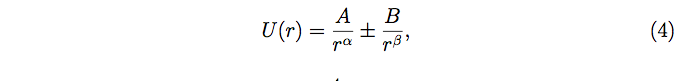
where r is the distance between the bodies, and A, B, α and β are positive constants. These kinds of potentials are called quasi-homogeneous. Expression (4) generalizes several well-known quasi-homogeneous potentials which model problems in biology, astrophysics, or chemistry as such as Birkhoff, Manev, Van der Waals, Libhoff, Schwarzschild, Lennard-Jones, the classical Newton, and Coulomb (see Sthephani et al., 2003).

Using any of those potentials, equation (2) becomes more difficult than with the Newtonian potential, since even the Kepler problem does not have an analytical solution. All this forces us to look much deeper for tools to get answers. Although this search is a very thorny road, the reward is amazing.

These findings are described in the article entitled Relative equilibria in quasi-homogeneous planar three-body problem, recently published in the journal Advances in Space Research. This work was conducted by John A. Arredondo from Fundación Universitaria Konrad Lorenz.