Can Rotating Hot Plasma Jets In The Solar Corona Become Unstable?

Solar jets are small-scale eruptions of hot plasma flowing along vertical or slightly oblique magnetic field lines. They are ubiquitous in the solar atmosphere from the photosphere to the outer corona. Solar jets are always associated with micro-flares that transfer magnetic energy to heat and kinetic energy.

The occurrence rate of jets is very high in the solar atmosphere and they could ee considered as a possible candidate source for heating the coronal plasma and accelerating the fast solar wind. The rotating, tornado-like, solar jets are among the most spectacular events in the solar atmosphere. Since their first observations by various instruments in the coronal hole regions, a very remarkable progress have been made to understand the physics of these solar jets by means of the high-resolution data of the Solar Dynamics Observatory (SDO) spacecraft.

Solar jets, in general, support the propagation of magnetohydrodynamic (MHD) waves which can become unstable against the so-called Kelvin–Helmholtz instability (KHI). It has been known for a long time that when the fluids of different speeds flow in the same direction, there will be a strong velocity shear near the interface region of two different speeds. This velocity shear produces a vortex sheet at the boundary which is indicative of the KHI occurrence.

Using the multi-wavelength data from the Atmospheric Imaging Assembly (AIA) on board the SDO, Chen et al., have studied a rotating jet occurring in a coronal hole near the northern pole of the Sun. AIA 304 Å images shown in the figure above (see also the movie) illustrate the detailed evolution of the jet (Zhelyazkov et al.). The small moving blobs on the right side boundary of the jet as indicated by white arrows could be produced by a KHI. The speed of the blobs was found to be of 120 ± 8 km/s, while their temporal evolution in the initial instability stage turned out to be about 2–4 min.

This rotating solar jet can be modeled as a vertically moving with velocity U weakly twisted magnetic flux tube of radius a = 9.8 × 10³ km, electron number density n_jet = 1.0 × 10⁹ cm^–3, temperature T_jet = 1.6 MK, surrounded by a static coronal plasma with n_cor = 0.9 × 10⁹ cm^–3, T_cor = 1.0 MK, and magnetic field of 3 G. In cylindrical coordinates (r, φ, z), the twisted jet magnetic field is given by B = (0, B_φ(r), B_z). The rotating speed is similarly presented as U = (0, U_φ(r), U_z). The twists of both magnetic field and flow velocity are characterized by the parameters ε₁ = B_φ/B_z and ε₂ = U_φ/U_z, respectively, where the azimuthal components B_φ and U_φ are evaluated at the tube surface, r = a. With measured U_z = 114 km/s and U_φ = 136 km/s, ε₂ = 1.2.

The propagation of the MHD modes crucially depends on the density contrast, η, between the jet and its environment. Defining η as n_cor/(n_jet + n_cor), we have η = 0.474. Another important parameter is the ratio of axial magnetic field components, b, of the external to the internal one (in our case is it b = 1.21), as well as the Alfvén speed inside the jet, v_A ≈ 150 km/s. Assuming that all perturbations, associated with the waves propagation behave like exp[i(–ωt + mφ + k_zz)], where ω is the angular wave frequency, m the azimuthal mode number, and k_z the axial wave number, one can show that the MHD wave propagation is governed by the so called dispersion relation D(ω, m, k_z, a, η, b, ε₁, ε₂, U_z, v_A) = 0, where, in searching for instability conditions, we consider the wave frequency as a complex quantity: ω = ω + iγ.

The solutions to the above dispersion equation were sought as dependencies of the normalized with respect to the Alfvén speed wave phase velocity v_ph/v_A = ω/(k_zv_A) on the normalized wavenumber k_za. Since we assume the wave frequency to be a complex quantity, we should obtain a pair of two functions of k_za: one for the Re(v_ph/v_A) and another for Im(v_ph/v_A). We assume that the KHI occurs at the registered axial jet velocity U_z = 114 km/s, which normalized with respect to v_A yields an Alfvén Mach number M_A = 0.76.

Concerning the twist of the jet magnetic field, we chose it to be relatively small, that is, ε₁ = 0.005. Under these input parameters, along with the aforementioned values of η, b, and ε₂, the numerical analysis of the dispersion equation shows that there exist finite-size instability regions in the 1D k_za-space. The width and the position of such an instability window depend primarily on the mode number m. If we expect the wavelength of the unstable MHD mode, λ_KH, to be of the order of 10 to 12 Mm (roughly the semi-width of the jet), such a KHI can happen at m = 12. The discussed dependencies above are presented graphically in Figure 1.

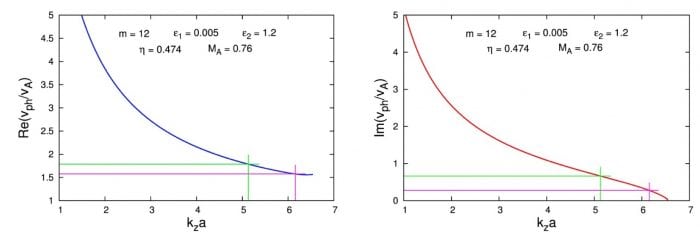
Figure 1. Dispersion curves and growth rates of the m = 12 MHD mode. The cross sections of purple lines define the normalized real and imaginary parts of the wave phase velocity at λKH = 10 Mm, while those of the green lines do the same for λKH = 12 Mm. Republished with permission from Elsevier from https://doi.org/10.1016/j.asr.2017.06.003.

From the dimensionless wave phase velocities and growth rates at the fixed two unstable wavelengths, we find in absolute units the corresponding frequency growth rates, γ_KH , and the instability growth/evolution times, τ_KH = 2π/γ_KH , as well as the wave phase velocities:

λ_KH = 10 Mm ⇒ γ_KH = 26 × 10^–3 s^–1; τ_KH ≈ 4 min;    v_ph ≈ 236 km/s

λ_KH = 12 Mm ⇒ γ_KH = 52 × 10^–3 s^–1; τ_KH ≈ 2 min;    v_ph ≈ 267 km/s

Note that the evaluated time intervals for the development of the KHI for both wavelengths are τ_KH ≈ 4 min and ≈2 min, which coincide with the observationally found temporal evolution times of the blobs in their initial stage.

Computations show that the width of the instability window becomes narrower with increasing the magnetic field twist parameter ε₁—actually the right-hand-side limit of the instability range shifts to the left. This implies, however, that generally, the unstable wavelengths become longer and at some critical ε₁ the shortest wavelength rolls out equal to the jet’s height H = 179 Mm. For a magnetic field twist bigger than the critical ε₁ one cannot speak for wave phenomenon at all. Hence, there exist a fixed left-hand-side limit, (k_za)_lhs, of the instability range, defined by the expression (k_za)_lhs ≡ 2πa/H = 0.344. This process of narrowing of the instability range with the increasing of ε₁ is clearly illustrated in the right panel of Figure 2.

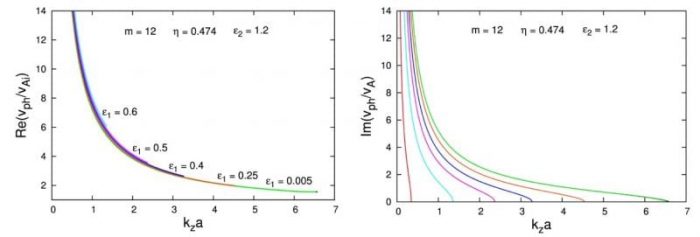
Figure 2. Real/observable m = 12 unstable MHD modes can be detected for ε1 < 0.68025, which implies that an azimuthal magnetic field of 1.7 G would suppress the KHI onset. Republished with permission from Elsevier from https://doi.org/10.1016/j.asr.2017.06.003.

The red curve there is obtained at k_za = 0.344 with  and for this value of ε₁ the width of the instability window is zero. On the other hand, from the definition of ε₁, it follows that an azimuthal magnetic field  would suppress the instability onset. With B_z = 2.45 G that azimuthal magnetic field is equal to ≈1.7 G. Thus, the answer to the question raised in the title, is “Yes”, if the magnetic field twist is not too strong. Otherwise, a big enough azimuthal magnetic field component of 1.7 G can suppress the KHI occurrence.

These findings are described in the article entitled Kelvin–Helmholtz instability in a twisting solar polar coronal hole jet observed by SDO/AIA, recently published in the journal Advances in Space Research. This work was conducted by Ivan Zhelyazkov (Sofia University), Teimuraz Zaqarashvili (University of Graz), Leon Ofman (NASA Goddard Space Flight Center), and Ramesh Chandra (Kumaun University).