How Neurons Synchronize In Human Oscillating Systems

Synchronization is a phenomenon that is present in many biological processes such as neurons when performing tasks. However, the phenomenon can also be observed in everyday activities, for instance when experiencing an applause. Initially, this starts out as so-called white noise, where there is no structure between each member, but after a while, you begin to hear a rhythmic clapping among the audience: they have synchronized.

Whether synchronization appears by some external forcing, such as circadian clocks which follows a 24h clock due to changes in daylight, or whether it appears by some intrinsic mechanism, such as in the applause example, synchronization is an interesting phenomenon to study. Especially within the area of neuroscience, where the quest is ongoing to map out networks of connected neurons that transmit information among each other. Our research on oscillating systems illustrates how to infer a network structure among coupled processes, such as neurons, by exploiting the class of statistical models known as cointegration models.

These models have originally been developed for, and are extensively used in, econometrics [1]. It is therefore well known theoretical results that we have applied in a new context. Roughly speaking cointegration means that two or more stochastic processes [2] share one or more common trends. This implies that if there is no cointegration, the processes will not influence each other, but contrary to this when cointegration is present each process in the system is influenced by the system as a whole.

We, therefore, argue that we can interpret a system of coupled neurons that synchronize, as a stochastic system that shares common trends and where each process is being pushed around by a force that is equivalent to a linear combination of the rest. This allows for the cointegration interpretation and thus opens up the theoretical toolbox of methods to estimate parameters and perform statistical inference for these models. Using this approach, we have demonstrated how to infer a network structure among 3 neurons in 4 cases (see Figure 1):

1. A system of independent (uncoupled) neurons.
2. A system where two neurons are coupled uni-directionally: neuron 2 influence neuron 1, but not the other way around. Neuron 3 is independent of these two.
3. A system where two neurons are coupled bi-directionally: neuron 1 and 2 influence each other and neuron 3 is independent of these two.
4. And all-to-all coupling, where all 3 neurons are coupled bi-directionally.

For each system, we simulated network activity and then analyzed the network structure, and in each case, we were able to derive the underlying structure, including the uni-directional coupling. The latter is usually a difficult case and is only possible when using non-symmetrical measures as opposed to symmetric measures, such as correlation. Figure 2 shows how the so-called phase processes behave in the 4 systems.

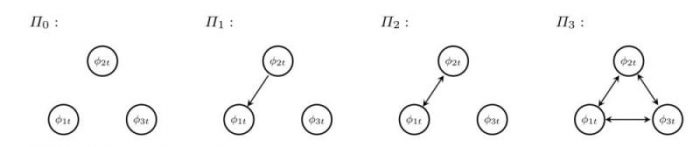
Figure 1: 4 systems of coupled neurons. Republished from Springer open access article: https://doi.org/10.1007/s00285-017-1100-2

Top left: the independent system, where the 3 neurons do not interact. The phases evolve independently of each other, although neurons 2 and 3 have similar slopes. Top right: the uni-directional case of two coupled neurons, here the phase of neuron 1 (green) is attracted to neuron 2 (orange), but not the other way around. Compare neuron 1’s phase with the dashed green line which is the reference to the independent system. Bottom left: the bi-directional case of two coupled neurons. The phases of neurons 1 (green) and 2 (orange) are attracted to each other and meet between their references for the independent system (dashed lines). Bottom right: all phases are attracted to each other in the all-to-all coupled system and therefore differ compared to their independent references (dashed lines).

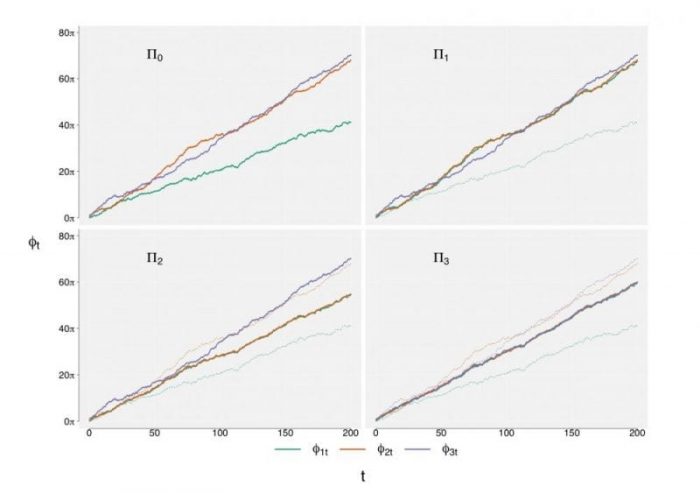
Figure 2: Phase processes of the 4 coupled systems. Republished from Springer open access article: https://doi.org/10.1007/s00285-017-1100-2

The significance of our demonstration is illustrated by analyzing a system of EEG data from epileptic patients where we demonstrate how the network connectivity changes within and outside seizure periods. Cointegration is a well-proven concept and applying this to neural data is relatively straightforward. It is, therefore, a powerful tool for future use in neuroscience which can assist experimental researchers in inferring connectivity of recorded neurons. Our research within cointegration models is currently ongoing with the aim of adapting these analysis methods to high-dimensional networks. The research described here has been published in the Journal of Mathematical Biology.

Notes:

1. In 2003 Clive Granger received the Economic Nobel prize for his work on cointegration models.
2. In our context, a stochastic process is a continuous time process that is driven by both a deterministic and a random component.

These findings are described in the article entitled Oscillating systems with cointegrated phase processes, published in the Journal of Mathematical Biology. This work was led by Jacob Østergaard, Anders Rahbek & Susanne Ditlevsen from the University of Copenhagen.