From Quantum Mechanics To Brain Neurostimulation: Abnormal Synchronization Of Neuronal Activity

Life has been considered for a long time as the most fascinating expression of the complexity of our universe, and the human brain is at the top of such complexity. In fact, compared to the difficulty of understanding the functioning of our brain, the laws of astrophysics are a piece of cake.

Neuroscientists — a new kind of scientist born as a hybrid crossover between a biologist, a physicist, a computer scientist, and a mathematician — have modeled for a long time the activity of each neuron as a simple mechanical oscillator coupled to many others through axons and dendrites. From this point of view, different parts of our brain correctly function when their “oscillators” are working synchronously as a whole and at the same time — whenever this is necessary — in synchrony with neurons of other parts of the brain (observe that such feature cannot last indefinitely because the brain should be able to skip to other tasks).

However, such perfect clock is sometimes abruptly broken by often unknown reasons. This is the case, for instance, when cells in the basal ganglia, placed deep in the inner brain, suddenly start to die. These cells are responsible for secreting up to 70% of the dopamine, and lack of this important neurotransmitter will cause unexpected and severe synchronized states yielding undesired symptoms such as shaking, rigidity, slowness in motions, mood or thought disorders all residing under the same umbrella of the Parkinson’s disease. History repeats itself also for the case of epilepsy, although here the neuropathological causes are still largely unknown.

In the latter case strong and — most importantly — unpredictable epileptic seizures affect the patient sometimes causing him severe physical injuries. Abnormal synchronization of neural activity has been thought to be the case also for other neurological disorders such as obsessive-compulsive disorder, Tourette syndrome, and chronic pain, just to mention few. Different attempts have been done to understand the underlying biochemical mechanisms that are at the root of such phenomena although we are still far from reaching a satisfactory goal. As a consequence, the aim of neurologists has consisted at least to ease the suffering patients by controlling the symptoms.

For a patient who is in the initial phase of Parkinsonism, oral medications may effectively work, but as the illness advances, they become less and less effective. For epilepsy instead, the situation is even worse with most of the actual medication presenting severe side effects.  Based on this scenario scientists have developed alternative solutions which are based on invasive neurostimulation to control the symptoms. In other words, these techniques consist in sending an electric signal through electrodes deeply implanted in the brain as for Parkinson’s or in the cortex for the epileptic disorders. Although invasive neurostimulation may look like a desperate and unorthodox attempt to approach a cure, with the tremendous evolution achieved recently in robotic surgery and nanomaterials, such techniques are becoming more and more common and at the same time less and less invasive.

Mathematics of neurostimulation

The neurostimulation presents an interesting challenge from the mathematical point of view. Indeed knowing how to optimally stimulate the brain in order to desynchronize the neuronal activity still remains an open problem in neuroscience. A seminal work has been done by P. Tass and coworkers at the Julich Institute in Germany to afford such problem. In particular, they have developed several feedback control methods to promptly desynchronize the coupled neurons; moreover, such methods have been shown to be effective even in the experimental setting of Parkinson macaque monkeys. Defining rigorously the optimal shape of the neurostimulation signal, is, however, a difficult and tricky task since a constant electric signal with large amplitude or high frequency is harmful not only to the neural patch where it is applied causing the death of the  surrounding cells but also may yield to severe counter effects such as hypersexuality.

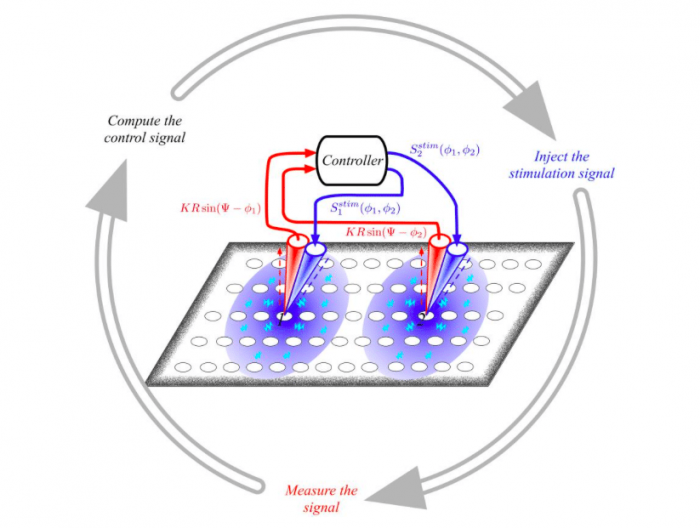
Republished from PLoS Computational Biology

To this aim, in our study, we have organized the search for the optimal neurostimulation in two phases: initially, we have mathematically identified the exact signal shape able to fully desynchronize each neuron once every unity is controlled with the less invasive signal as possible; and then, we have efficiently adapted this formula to a feasible setting where the number of neural patches directly controlled is limited to just a few and no global knowledge of the involved neurons is needed.

Hamiltonian control as a desynchronization method

Finding an innocuous mathematical signal shape able to neutralize the strong coupling which brings to synchronization sounds counter-intuitive at all. And indeed it is when we look at the problem from the classical point of view. But if we restore to a higher formalism such as Hamiltonian mechanics things become more clear. Hamiltonian mechanics is an abstract mathematical framework to cover all kind of conservative motions and interactions that occur in nature spanning from classical to relativistic physics, from the motion of celestial bodies to that of microscopical quantum particles.

Working in this field, M. Vittot from Marseille (France), rigorously proved that a multibody Hamiltonian system can be effectively controlled using terms whose order is smaller than the coupling among the system parts. This result is simply amazing! In few words, it states that the strength we need to put things apart is much smaller than that of keeping them all together. Vittot and coworkers have successfully applied this result to quantum control or to a particle accelerator. On our side, based on his theorem, we could recover the minimal function needed to desynchronize coupled neurons after properly reformulating the problem of brain dynamics in terms of the Hamiltonian mechanics.

Effectively controlling abnormal brain activity

Controlling abnormal synchronization activity of the neurons is not only a mathematical question but also a practical one. Our initial result could be used to perfectly desynchronize abnormal brain activity but it needs to access each neuron one by one. This, of course, is not possible in practice. To tackle this issue we trimmed the control term to the bone, cutting out any “unnecessary” terms in such a way to eventually obtain a new function which depends only on the variables of the neuronal patch where the electrode is applied. In other words, the efficient control consists of the signal measured from the neuronal patches, which is delayed by a quarter of the period of the recorded signal, multiplied by a suitable constant and reinjected again in the same neuronal patch. At the same time, each electrode generates an exponentially decaying electromagnetic field, because of the signal, which would indirectly affect the activity of the other nearby neurons.

Astonishingly the so obtained control is effective as we a posteriori verified by numerical simulations. The new term is still much smaller than the  original coupling one and its main advantage is that when no abnormal symptoms are present the control term is also almost invisible not affecting at all the brain activity; however when seizures, as is the case for epilepsy, emerge then the control term also increases its size and becomes activated. This way we are introducing a “hidden” feedback which does not depend at all at any global measure of the neurons’ activity, a measure which cannot be actually obtained and upon which previous methods have been rooted. Our control is indeed implicit to the brain activity minimizing at maximum any side effect.

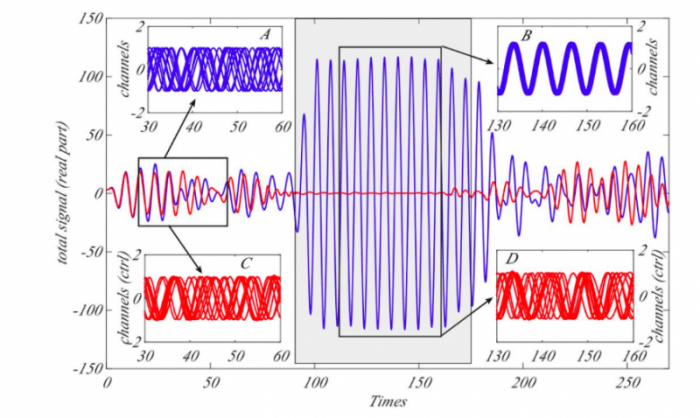
Republished from PLoS Computational Biology

In our study, we aim to do the first step in further understanding the optimal desynchronization protocols of abnormal brain activity opening to future works intending more sophisticated approaches to this problem.

These findings are described in the article entitled Using Hamiltonian control to desynchronize Kuramoto oscillators, previously published in the journal Physical Review E. This work was also described in the article entitled A minimally invasive neurostimulation method for controlling abnormal synchronisation in the neuronal activity, recently published in the journal PLoS Computational Biology. To this research contributed Oltiana Gjata and Luigi Barletti from the University of Florence, Italy, Paul Expert from Imperial College of London, UK, and Malbor Asllani and Timoteo Carletti from the University of Namur, Belgium.